Combinatorial Optimization and Fitness Landscape Analysis
Scope and Objectives:
Local search based meta-heuristics like Simulated Annealing, Tabu Search and Genetic Algorithms have been successfully applied to many combinatorial optimization problems. Still research is unable to explain adequately why or when an algorithm is likely to succeed or fail. It has been shown empirically that no approach cuts out its rivals in solving different combinatorial problems. Even when applied to different instances of the same problem type often no algorithm is superior. But, as a matter of experience, the performance of local search often depends on the configuration of the underlying search space.
Short Description:
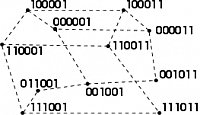
The set of feasible solutions to an optimization problem is structured by neighbourhoods that define a set of possible moves from each single solution. As shown in the picture, solutions can be represented by nodes of a graph and moves between solutions can be represented by edges. Every node of the graph is assigned a value from the objective function of the problem. The resulting node-weighted graph is also called a fitness landscape of the problem under consideration. The structure of a fitness landscape sheds some light on the issue of problem difficulty for local search. In general, rugged landscapes with widely spread local optima and low fitness-distance correlation are expected to be difficult for local search. Despite extensive analyses of fitness landscapes for various combinatorial optimization problems, the link between problem difficulty and fitness landscape structure is hardly understood. Commonly there are two ways to a treat combinatorial optimization problem with a complex fitness landscape. One is to introduce sophisticated types of moves, which smooth the search space to bypass barriers separating the various local optima. The other is to use control-parameters in the meta-heuristic which allows deteriorating moves in order to climb over the barriers. Due to limitations of theoretical analysis, statistical measures of landscapes are proposed arguing that the success of local search is predictable on the basis of key indicator for search space structure. In this research project we investigate the problem specific expression of these statistical measures while particularly addressing scheduling problems.
Project Duration:
Research started in 1996
Main Literature:
- Weinberger, E.: Correlated and Uncorrelated Fitness Landscapes and How to Tell the Difference. Biological Cybernetics, 63 (1990) p. 325-336
- Kauffmann, S.A..: The Origins of Order. Oxford University Press, 1993, NY
Contact:
Prof.-Dr. Christian Bierwirth (christian.bierwirth@wiwi.uni-halle.de)
Publications and Talks:
- Bierwirth, C.: Das Konzept der Fitnesslandschaft als Methode zur Beurteilung der Schwierigkeit von kombinatorischen Optimierungsproblemen, In: Bortfeldt, A.; Homberger, H.; Kopfer, H.; Pankratz, G.; Strangenmeier, R. (Eds.): Intelligente Entscheidungsunterstützung, Gabler Edition Wissenschaft, Wiesbaden, 2008, 287-302
- Bierwirth, C., Mattfeld, D.C., Watson, J.P.: Landscape Regularity and Random Walks for the Job Shop Scheduling Problem. Lecture Notes in Computer Science 3004 (2004) p. 21-30
- Mattfeld, D.C., Bierwirth, C., Kopfer, H.: A Search Space Analysis fort he Job Shop Scheduling Problem. Annals of Operation Research 86 (1999) p. 441-453




