Kombinatorische Optimierung und Fitnesslandschaft-Untersuchungen
Gegenstand und Ziele:
Auf lokaler Suche basierende Meta-Heuristiken wie Simulated Annealing, Tabu Search und Genetische Algorithmen lassen sich für viele kombinatorische Optimierungsprobleme erfolgreich einsetzen. Dennoch ist die Forschung bis heute nicht in der Lage, adäquat zu erklären, wann oder warum die Anwendung eines Algorithmus zum Erfolg führt oder fehlschlägt. Allerdings konnte empirisch gezeigt werden, dass es keinen dominanten Algorithmus für alle Problemklassen gibt. Selbst bei der Anwendung auf verschiedene Instanzen desselben Optimierungsproblems stellt sich meist kein Algorithmus als überlegen heraus. Die Erfahrung zeigt jedoch, dass die Lösungsgüte der lokalen Suche von der Konfiguration des darunter liegenden Suchraums beeinflusst wird.
Kurzdarstellung:
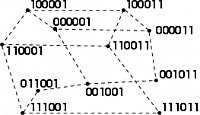
Die Menge zulässiger Lösungen eines Optimierungsproblems wird durch Nachbarschaften strukturiert, die für jede Lösung eine Teilmenge benachbarter Lösungen beschreiben, welche durch so genannte "Moves" aus der ursprünglichen Lösung hervorgehen. Wie im Bild gezeigt, können unterschiedliche Lösungen als Knoten in einem Graph dargestellt werden, wobei die "Moves" zwischen Lösungen durch Kanten repräsentiert sind. Jedem Knoten des Graphen wird durch die Zielfunktion des Problems ein Zielfunktionswert zugeordnet. Der resultierende knoten-gewichtete Graph beschreibt eine Fitnesslandschaft für das betrachtete Problem. Die Struktur der Fitnesslandschaft beleuchtet in anschaulicher Weise die Frage nach dem Schwierigkeitsgrad, mit dem ein lokales Suchverfahren konfrontiert wird. Im Allgemeinen erscheinen Landschaften mit vielen weit verstreuten lokalen Optima und geringer Fitness-Distanz-Korrelation als schwer zu lösende Probleme für eine lokales Suchverfahren. Trotz der Erforschung von Fitnesslandschaften unterschiedlicher kombinatorischer Optimierungsprobleme existieren keine gesicherten Kenntnisse über den systematischen Zusammenhang zwischen dem Schwierigkeitsgrad einer Aufgabe und der Struktur der zugehörigen Fitnesslandschaft. In der Literatur werden zwei Wege unterschieden, um kombinatorische Optimierungsprobleme mit komplexen Fitnesslandschaften zu lösen. Eine Möglichkeit besteht in der Entwicklung problemspezifischer Nachbarschaften, die den Lösungsraum aufgrund spezieller "Moves" gewissermaßen "glätten" und somit Barrieren zwischen lokalen Minima abbauen. Eine andere Möglichkeit ist es, Steuerungsparameter für die verwendete Meta-Heuristik zu definieren, wodurch temporäre Verschlechterungen bei der lokalen Suche zugelassen werden, um Barrieren zwischen den Optima überwinden zu können. Aufgrund des unzureichenden theoretischen Verständnisses werden vielfach statistische Kennzahlen für die Beschreibung einer Fitnesslandschaft herangezogen. Ziel ist es hierbei, die Zweckmäßigkeit und damit den Erfolg eines lokalen Suchverfahrens auf der Basis der beobachteten Indikatoren abschätzen zu können. Das Forschungsprojekt untersucht die problemspezifische Aussagekraft von Kennzahlen für Fitnesslandschaften am Beispiel von Schedulingproblemen.
Projektzeitraum:
seit 1996
Basisquellen:
- Weinberger, E.: Correlated and Uncorrelated Fitness Landscapes and How to Tell the Difference. Biological Cybernetics, 63 (1990) p. 325-336
- Kauffmann, S.A..: The Origins of Order. Oxford University Press, 1993, NY
Kontakt:
Prof.-Dr. Christian Bierwirth (christian.bierwirth@wiwi.uni-halle.de)
Projektbezogene Publikationen und Vorträge:
- Bierwirth, C.: Das Konzept der Fitnesslandschaft als Methode zur Beurteilung der Schwierigkeit von kombinatorischen Optimierungsproblemen, In: Bortfeldt, A.; Homberger, H.; Kopfer, H.; Pankratz, G.; Strangenmeier, R. (Hrsg.): Intelligente Entscheidungsunterstützung, Gabler Edition Wissenschaft, Wiesbaden, 2008, 287-302
- Bierwirth, C., Mattfeld, D.C., Watson, J.P.: Landscape Regularity and Random Walks for the Job Shop Scheduling Problem. Lecture Notes in Computer Science 3004 (2004) p. 21-30
- Mattfeld, D.C., Bierwirth, C., Kopfer, H.: A Search Space Analysis fort he Job Shop Scheduling Problem. Annals of Operation Research 86 (1999) p. 441-453




